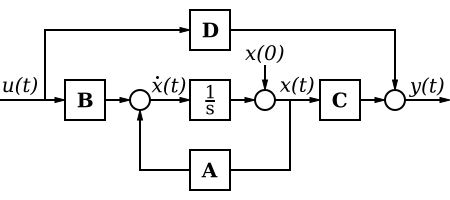
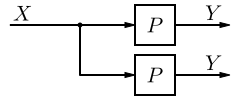
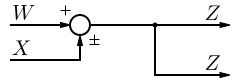
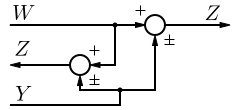
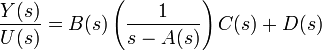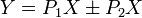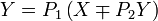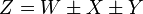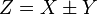A network diagram is a type of network. A network in general is an interconnected group or system, or a fabric or structure of fibrous elements attached to each other at regular intervals, or formally: a graph.
A network diagram is a special kind of cluster diagram, which even more general represents any cluster or small group or bunch of something, structured or not. Both the flow diagram and the tree diagram can be seen as a specific type of network diagram.

In computer science the elements of a network are arranged in certain basic shapes (see figure):
Source: http://en.wikipedia.org/wiki/Network_diagram
A network diagram is a special kind of cluster diagram, which even more general represents any cluster or small group or bunch of something, structured or not. Both the flow diagram and the tree diagram can be seen as a specific type of network diagram.
Types of network diagrams
There are different types network diagrams:- Artificial neural network or "neural network" (NN), is a mathematical model or computational model based on biological neural networks. It consists of an interconnected group of artificial neurons and processes information using a connectionist approach to computation.
- Computer network diagram is a schematic depicting the nodes and connections amongst nodes in a computer network or, more generally, any telecommunications network.
- In project management according to Baker et al. (2003), a "network diagram is the logical representation of activities, that defines the sequence or the work of a project. It shows the path of a project, lists starting and completion dates, and names the responsibilities for each task. At a glance it explains how the work of the project goes together... A network for a simple project might consist one or two pages, and on a larger project several network diagrams may exist" . Specific diagrams here are
- Project network: a general flow chart depicting the sequence in which a project's terminal elements are to be completed by showing terminal elements and their dependencies.
- PERT network
- Neural network diagram: is a network or circuit of biological neurons or artificial neural networks, which are composed of artificial neurons or nodes.
- A semantic network is a network or circuit of biological neurons. The modern usage of the term often refers to artificial neural networks, which are composed of artificial neurons or nodes.
- A sociogram is a graphic representation of social links that a person has. It is a sociometric chart that plots the structure of interpersonal relations in a group situation.
Gallery
-

Artificial neural network
Network topologies

Diagram of different network topologies.
- Full Mesh: Every node is connected to every other node. Most redundant and expensive.
- Partial Mesh Is similar to a full mesh, but some nodes still have to go through others to get to its final destination. Offers some redundancy and not as expensive as full mesh.
- Star: The star network consists of one central element, switch, hub or computer, which acts as a conduit to coordinate activity or transmit messages. Good redundancy and fairly cheap (most common).
- Ring: The ring network connects each node to exactly two other nodes, forming a circular pathway for activity or signals - a ring. The interaction or data travels from node to node, with each node handling every packet. Typically used by small businesses in a P2P design.
- Bus: In this network architecture a set of clients are connected via a shared communications line, called a bus network. Least redundancy and cost (single point of failure).
- Hybrid:Two or more topologies combined for example multiple stars connecting to a fiber backbone (the backbone being a bus topologies), or a ring and a star.
- Tree: This consists of tree-configured nodes connected to switches/concentrators, each connected to a linear bus backbone. Each hub rebroadcasts all transmissions received from any peripheral node to all peripheral nodes on the network, sometimes including the originating node. All peripheral nodes may thus communicate with all others by transmitting to, and receiving from, the central node only.
Source: http://en.wikipedia.org/wiki/Network_diagram











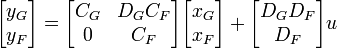



 or
or