When designing or analyzing a system, often it is useful to model the system graphically. Block Diagrams are a useful and simple method for analyzing a system graphically.
The control model uses the transformation process in the context of a technology system

The inputs consist of primary (raw materials) and secondary (energy, manufacturing plant, workforce). There are also primary and secondary output representing the main product and bi-products (worn out staff, spent resources etc) {Source1}
 If we have two systems, f(t) and g(t), we can put them in series with one another so that the output of system f(t) is the input to system g(t). Now, we can analyze them depending on whether we are using our classical or modern methods.
If we have two systems, f(t) and g(t), we can put them in series with one another so that the output of system f(t) is the input to system g(t). Now, we can analyze them depending on whether we are using our classical or modern methods.
If we define the output of the first system as h(t), we can define h(t) as:

 In the time domain we know that:
In the time domain we know that:
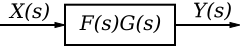
System 1:
 Blocks may not be placed in parallel without the use of an adder. Blocks connected by an adder as shown above have a total transfer function of:
Blocks may not be placed in parallel without the use of an adder. Blocks connected by an adder as shown above have a total transfer function of:

 In this image, the strange-looking block in the center is either an integrator or an ideal delay, and can be represented in the transfer domain as:
In this image, the strange-looking block in the center is either an integrator or an ideal delay, and can be represented in the transfer domain as:
{Source2}The control model uses the transformation process in the context of a technology system

The inputs consist of primary (raw materials) and secondary (energy, manufacturing plant, workforce). There are also primary and secondary output representing the main product and bi-products (worn out staff, spent resources etc) {Source1}
Systems in Series
When two or more systems are in series, they can be combined into a single representative system, with a transfer function that is the product of the individual systems.
If we define the output of the first system as h(t), we can define h(t) as:
- h(t) = x(t) * f(t)
- y(t) = h(t) * g(t)
- y(t) = [x(t) * f(t)] * g(t)
- y(t) = x(t) * [f(t) * g(t)]

Series Transfer Functions
If two or more systems are in series with one another, the total transfer function of the series is the product of all the individual system transfer functions.
- y(t) = x(t) * [f(t) * g(t)]
- Y(s) = X(s)[F(s)G(s)]
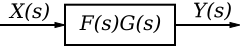
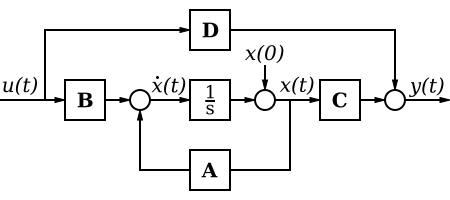
Series State Space
If we have two systems in series (say system F and system G), where the output of F is the input to system G, we can write out the state-space equations for each individual system.System 1:
- xF' = AFxF + BFu
- yF = CFxF + DFu
- xG' = AGxG + BGyF
- yG = CGxG + DGyF
[Series state equation]
[Series output equation]
Systems in Parallel

- Y(s) = X(s)[F(s) + G(s)]
- y(t) = x(t) * [f(t) + g(t)]

State Space Model
The state-space equations, with non-zero A, B, C, and D matrices conceptually model the following system:
 or
or 

In the Laplace Domain
The state space model of the above system, if A, B, C, and D are transfer functions A(s), B(s), C(s) and D(s) of the individual subsystems, and if U(s) and Y(s) represent a single input and output, can be written as follows:Adders and Multipliers
Some systems may have dedicated summation or multiplication devices, that automatically add or multiply the transfer functions of multiple systems togetherSimplifying Block Diagrams
Block diagrams can be systematically simplified.| Transformation | Equation | Block Diagram | Equivalent Block Diagram | |
|---|---|---|---|---|
| 1 | Cascaded Blocks |  |  |  |
| 2 | Combining Blocks in Parallel | 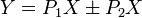 |  | 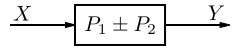 |
| 3 | Removing a Block from a Forward Loop | 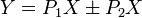 |  | |
| 4 | Eliminating a Feedback Loop | 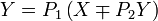 |  |  |
| 5 | Removing a Block from a Feedback Loop | 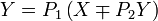 |  | |
| 6 | Rearranging Summing Junctions | 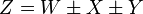 |  |  |
 | ||||
| 7 | Moving a Summing Juction in front of a Block |  |  |  |
| 8 | Moving a Summing Juction beyond a Block |  |  |  |
| 9 | Moving a Takeoff Point in front of a Block |  |  | 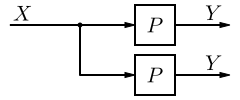 |
| 10 | Moving a Takeoff Point beyond a Block |  |  |  |
| 11 | Moving a Takeoff Point in front of a Summing Junction |  | 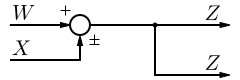 | 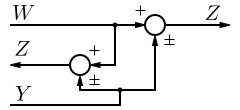 |
| 12 | Moving a Takeoff Point beyond a Summing Junction | 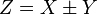 |  |  |
{Source1: http://www.mbanotes.org/node/9 }
{Source2: http://en.wikibooks.org/wiki/Control_Systems/Block_Diagrams }

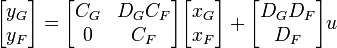
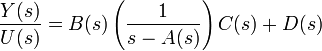
Howdy! This article couldn’t be written much better!
ReplyDeleteReading through this article reminds me of my previous roommate!
He always kept talking about this. I'll forward this information to him. Pretty sure he's going to have a very good read. Thank you for sharing! payday loans baton rouge
my web page - payday loans bad credit
Spot on with this write-up, I honestly feel this website needs far more attention.
ReplyDeleteI’ll probably be returning to read more, thanks for the info!
speaking of
my site - special info